tg-me.com/knowledge_accumulator/283
Last Update:
AlphaEvolve [2025]
Очень простым критерием, по которому я отсекаю интересные "приложения AI в науке" от неинтересных, это то, была ли в итоге решена какая-то нерешённая задача. Deepmind имеет неплохую репутацию в этом вопросе, и я уже писал посты про их подобные работы - AlphaTensor, AutoNumerics-Zero и некоторые другие.
Перед нами ещё одна работа, выбивающая SOTA на разного рода математических задачах. Я очень обрадовался, увидев первым автором Сашу Новикова, с которым когда-то капельку поработал, будучи ещё безмозглым пиздюком.
Итак, перед нами идейный потомок FunSearch. Это хорошо проделанная практическая работа по масштабированию, однако, основная идея изменилась не особо.
Алгоритм применим для поиска решений "NP-задач", т.е. в которых возможна быстрая (автоматическая) оценка решения. Это вариация эволюционного поиска программы, который поддерживает популяцию решений и вместо примитивных операций над кодом использует LLM для генерации новых кандидатов.
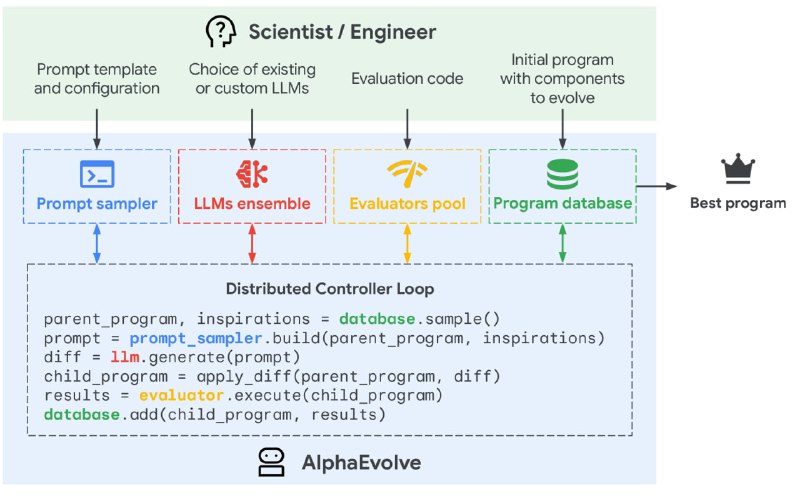
Дьявол, конечно, в деталях, и над ними как раз хорошо поработали. Тут тебе и комбинация разных LLM, и целая процедура генерации промпта, включающая параллельно оптимизируемый мета-промпт, и оптимизация диффа вместо программы, и LLM-generated feedback, и, конечно, reward design.
Последнее особенно важно. Дело в том, что эволюционный алгоритм применяется для оптимизации какой-то непрерывной награды. Если у вас есть 10000 вариантов, из которых 9999 одинаково неработающие и 1 работающий, то все эти алгоритмы умного перебора не имеют никакого смысла.
Ставя задачу "докажите утверждение X" в пространстве всех математических доказательств, у вас нет способа сравнить два неправильных черновика между собой. Но в некоторых случаях инструменты сравнения всё же имеются.
В качестве первого примера применения алгоритма в статье описан поиск способов умножать матрицы за меньшее число умножений - та же тема, что и в AlphaTensor. Любой алгоритм по умножению 2 матриц может быть представлен как разложение определённого 3D-тензора в несколько тензоров ранга 1. Количество тензоров в разложении и определяет количество умножений. Пишите в комментариях, если это враньё, я просто цитирую.
Как я понял, находить такие разложения можно с помощью градиентной оптимизации - тензоры в разложении оптимизируются градиентным спуском под то, чтобы результирующий тензор совпадал с желаемым.
Но нет, AlphaEvolve не оптимизирует разложение. Он генерирует алгоритм, генерирующий разложение. В качестве затравки ему как раз и даётся тот самый метод градиентного спуска, после чего AlphaEvolve пытается его модифицировать. И у получаемого кода есть отличная мера качества - минимальное количество тензоров, на которое получилось разложить.
Представьте, что самый базовый алгоритм может сгенерировать разложение на 50 тензоров, а разложение на 49 уже не сходится. Если кандидат от AlphaEvolve не сошёлся даже для 50, то сразу отправляется на помойку, но если вдруг смог разложить на 49, то получает более высокий скор в рамках эволюции. Каждый кандидат запускается последовательно на всё более сложной задаче - его просят разложить на 49, 48, 47 тензоров и т.д., и со временем получаются всё более и более крутые алгоритмы оптимизации.
В результате такого процесса авторам удалось отыскать с помощью улучшенной оптимизации кучу новых рекордно коротких разложений и сильно обойти AlphaTensor, который был заточен именно под эту задачу. В статье есть ещё много примеров успешных применений AlphaEvolve на практике, каждое из которых можно было бы разбирать отдельными постами.
Данная работа является крутейшим примером того, как LLM может быть использован для научных открытий. Нет, не надо генерировать вот эту срань. Нужно применить человеческую креативность для того, чтобы переформулировать "NP-задачу" в задачу генерации кода, который можно оценить непрерывным скором, и только потом дёргать LLM в качестве генератора кандидатов.
Но это пока кто-то не изобретёт что-нибудь получше.
@knowledge_accumulator
BY Knowledge Accumulator
Share with your friend now:
tg-me.com/knowledge_accumulator/283
